遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
简介
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。其基本操作算子有选择、杂交、变异。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
问题定义
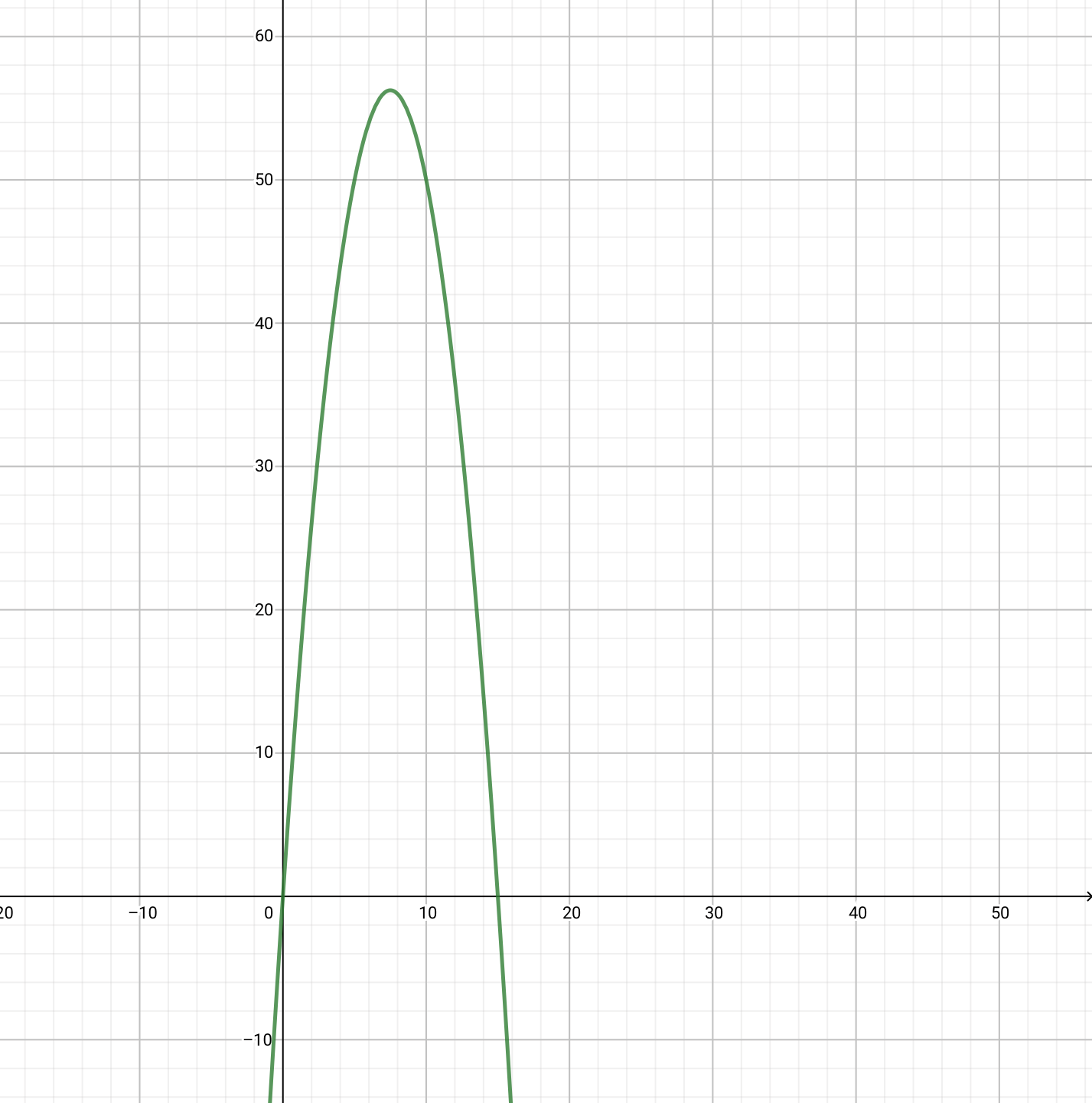
本文以解二次函数最值为例讲解遗传算法。
具体问题为:找到函数y=-x2+15x最大值对应的x是多少。
算法核心
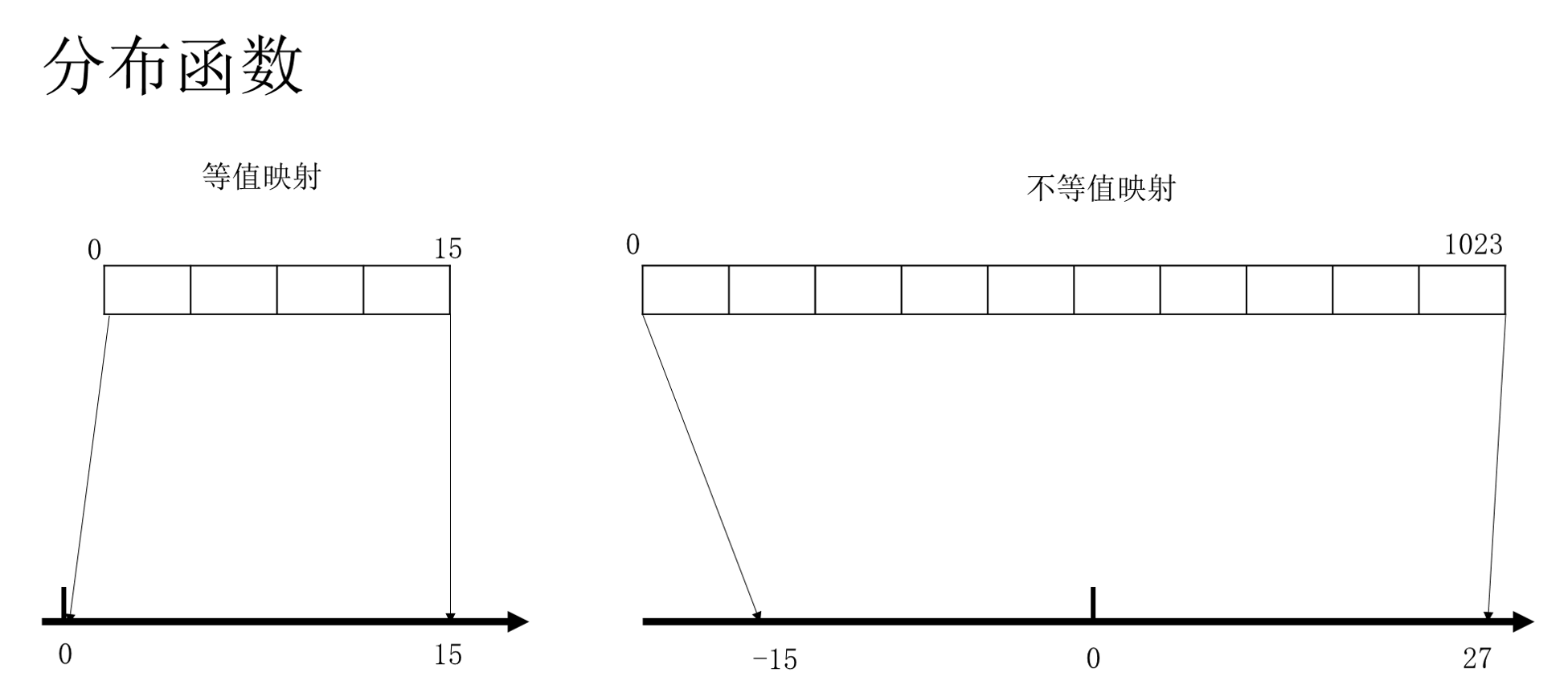
参数编码
将自变量x编码为二进制,染色体长度为4,全0表示0,引入分布函数,全1表示15,染色体表示的0~24-1被映射到0~15。(为了下文画图的便利而使用了等值映射,实际应当根据需要选择不同的映射方式)
初始群体的设定
这里随机初始化染色体
适应度函数
即 |-x2+15x|
遗传操作设计
详见算法流程图
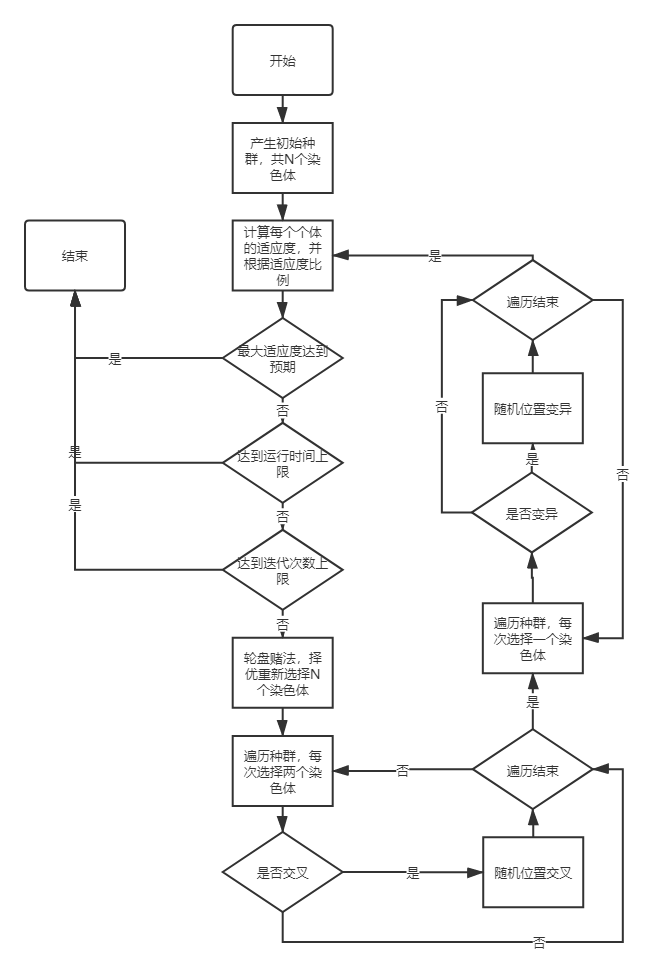
控制参数设定
编码长度为4(即染色体长度),种群数量为6,交叉概率(通常偏大),变异概率(通常极小),最大运行时间,最大迭代次数(通常为50~500)
选择算子
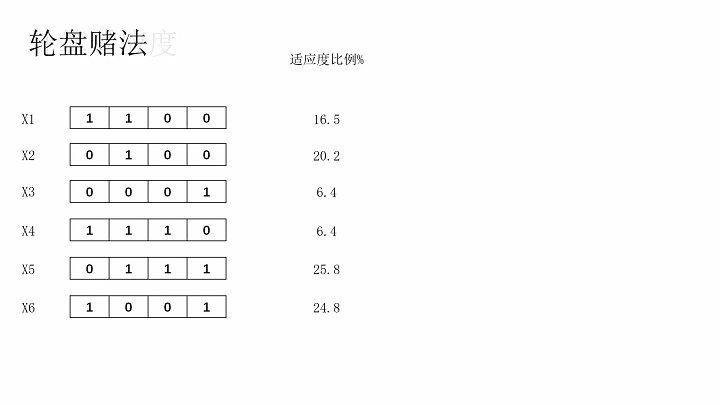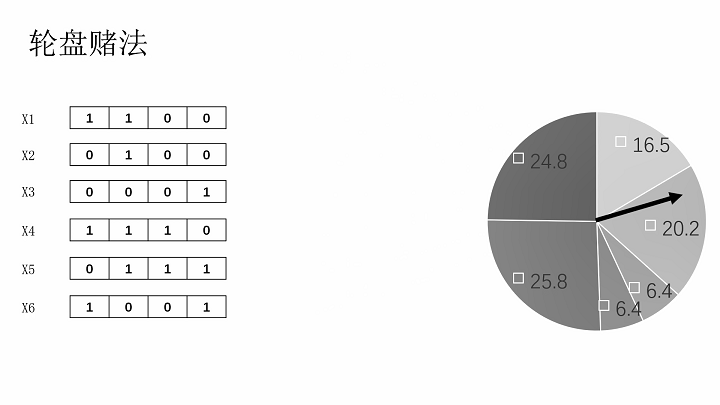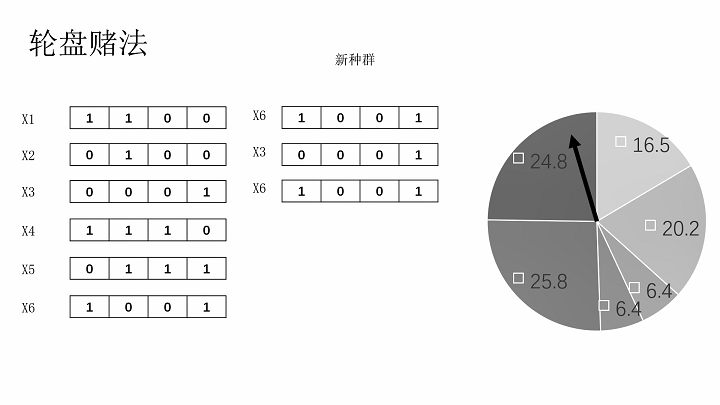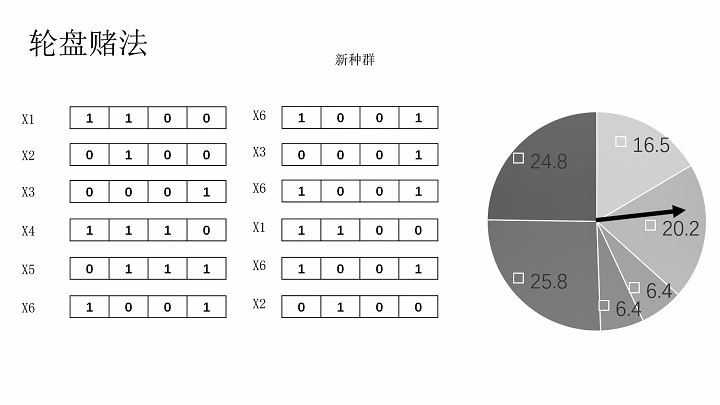
轮盘赌法。该算子模拟的就是商场抽奖的大转盘,在计算染色体适应度后,再计算适应度比例,比例越大的染色体在轮盘上占据的空间就越大。随后选取0~1的随机数,该随机数模拟指针,指到哪个染色体就选择哪个染色体。
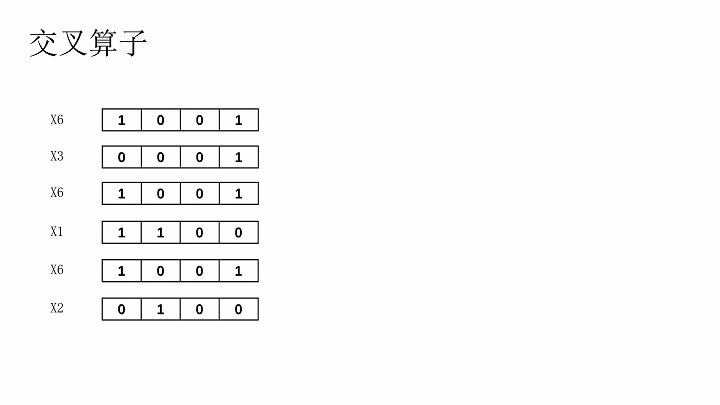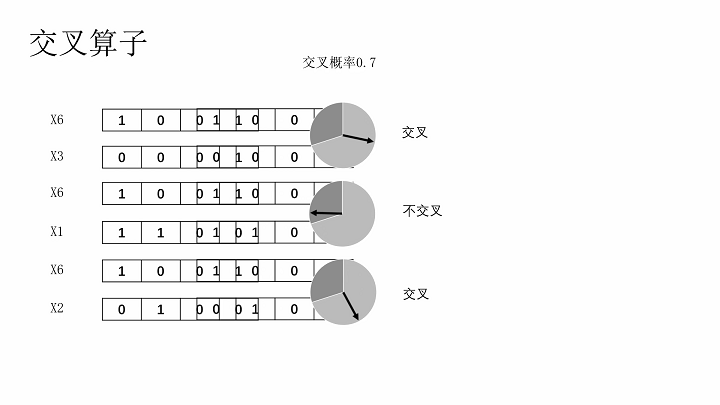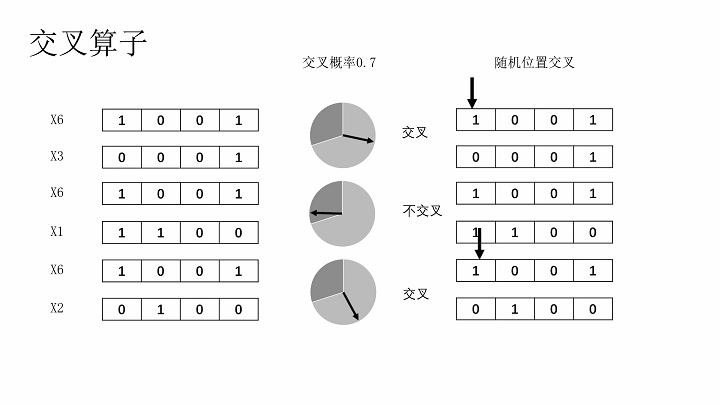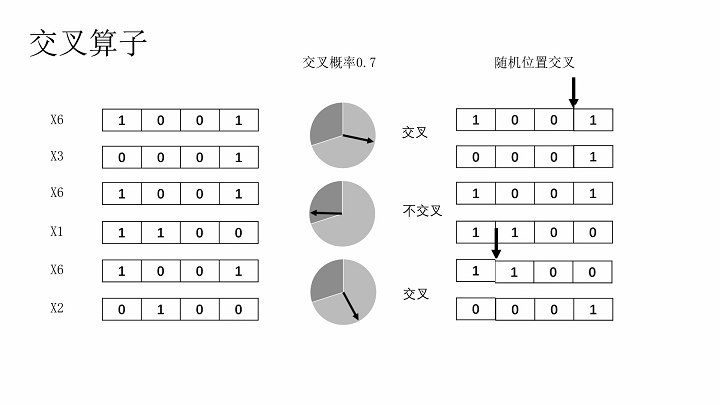
交叉算子
将两个染色体根据某种方式交叉部分基因,形成两个新的染色体。交叉方式有单点交叉、多点交叉、均匀交叉、算数交叉。本文选用单点交叉,及两个染色体在交叉时,随机选择一个相同的截断点,拆分后互换一半基因。
变异算子
单个染色体中的某个位置被任意其他元素取代。本文采用二进制染色体,变异即是取反。
实例动图演示
初始化种群
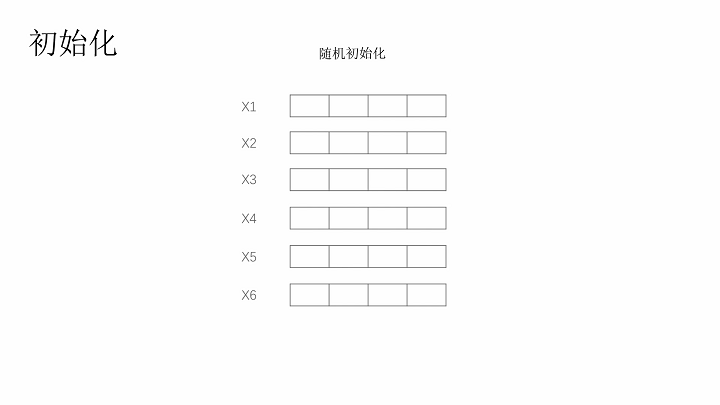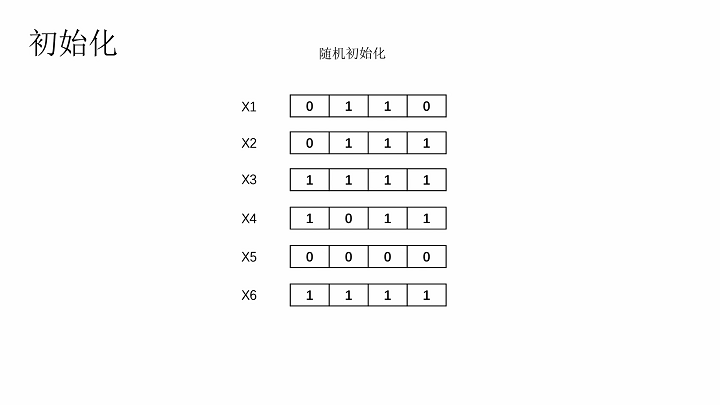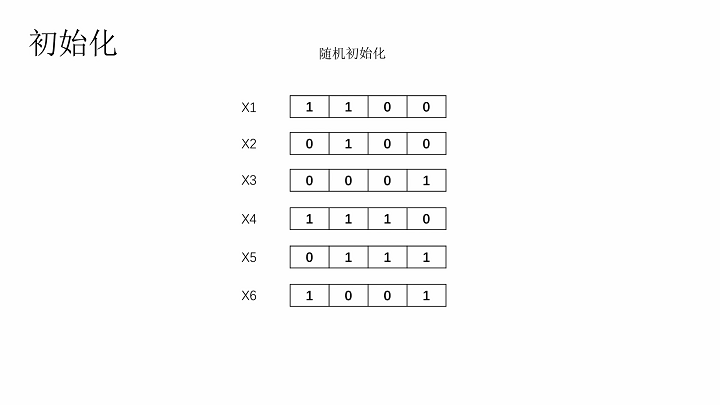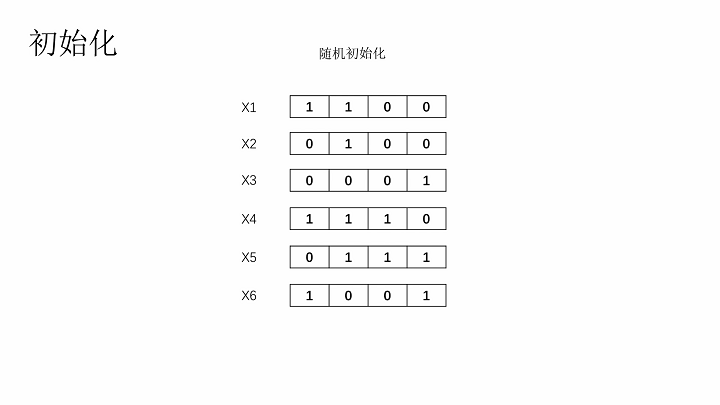
计算适应度、适应度比例
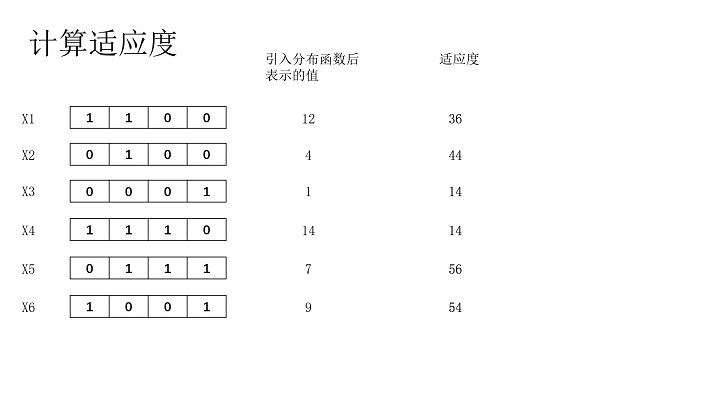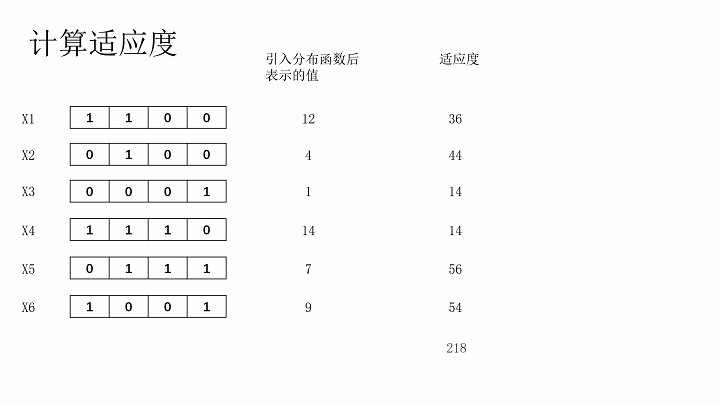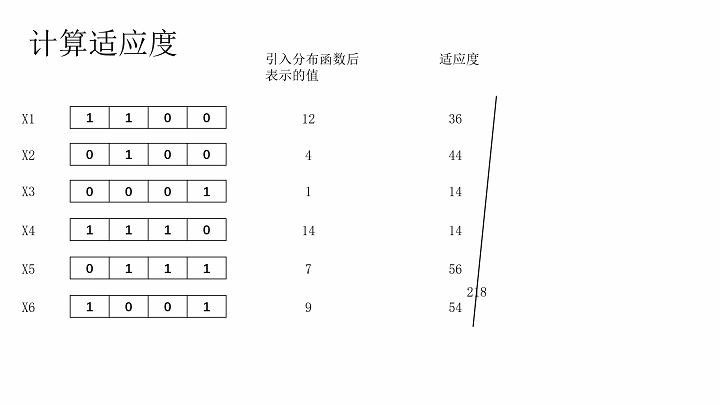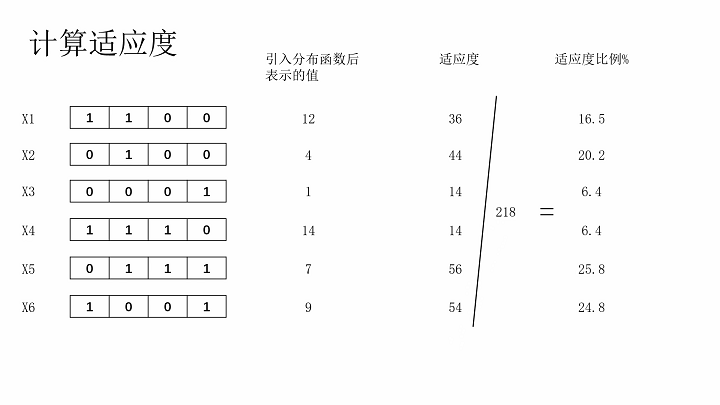
轮盘赌法择优选择染色体
交叉
变异

得到新种群
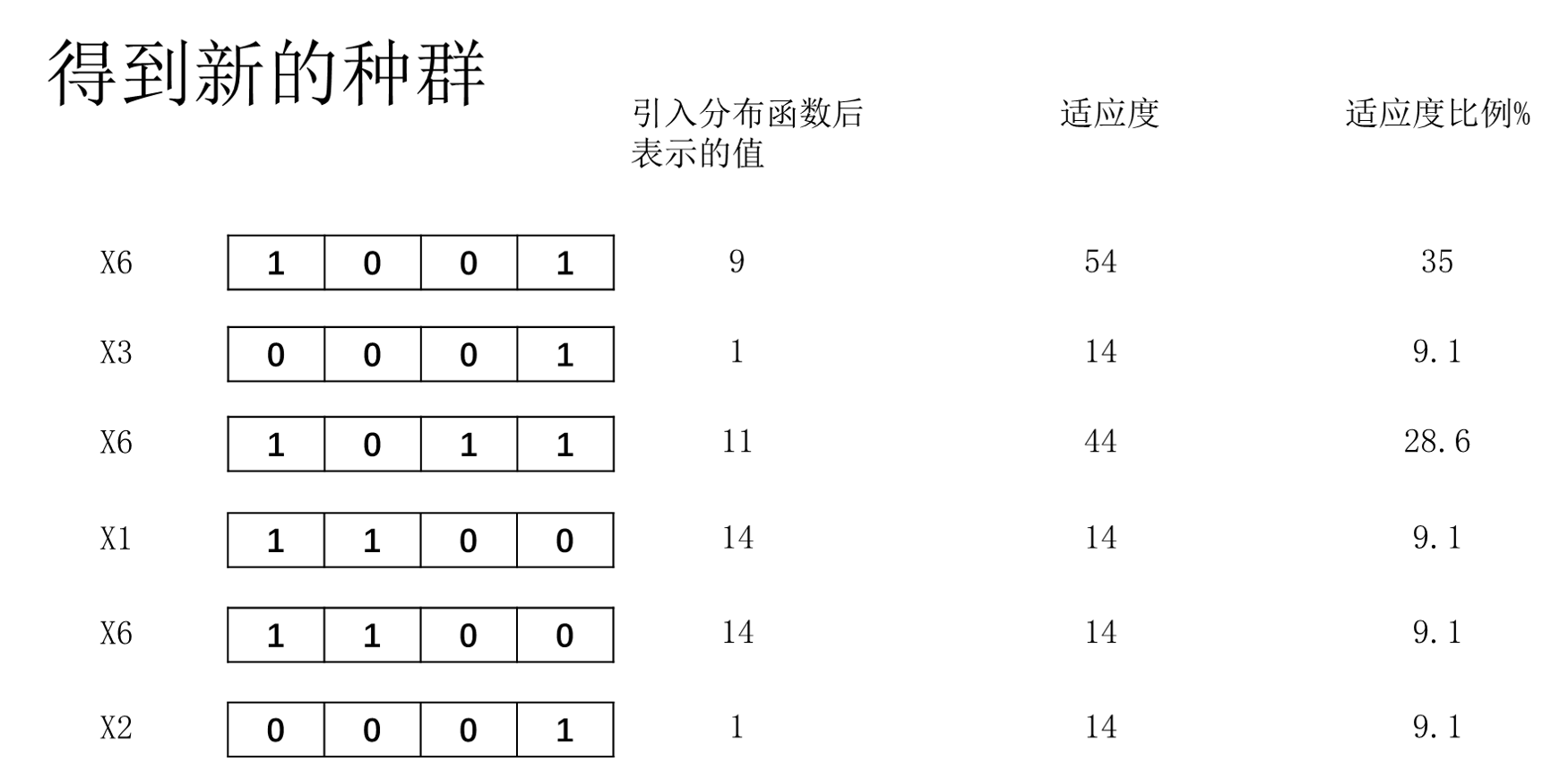
回到步骤2,直至满足退出条件