秘密是目前构建社会的必要元素之一。秘密天生需要保护性，失去保护的秘密便不再被称为秘密。保护秘密的方法有加密和隔离，本文讨论在存储、通信中保护秘密的加密体制之一——非对称加密体制。

简介

网络通信引入非对称密码体制

传统密码体制基本都是对称密码体制，也就是加密、解密使用同一个密钥。虽然对称密码体制可以通过数学、概率证明加密过程的高效性、结果的有效性，但是其最薄弱的点是密钥本身。如果A和B通信过程使用对称加密算法，意味着密钥本身是不能被其他人获取的。如果密钥由A产生，B获取密钥的方法有且只有一个——从A获取。为了保证密钥的安全，密钥一般是随机生成的。即是密钥是通过计算生成的，并假设有密钥协商过程。由于网络通信的不可信，协商的内容可以看作明文，B和其他所有人都没有或者都有相同的信息，要么B和其他所有人都能计算出密钥，要么都不能计算出密钥。由于对称密码体制的对称性，可以推出在传统密码体制下，没法安全地通过网络交换密钥。

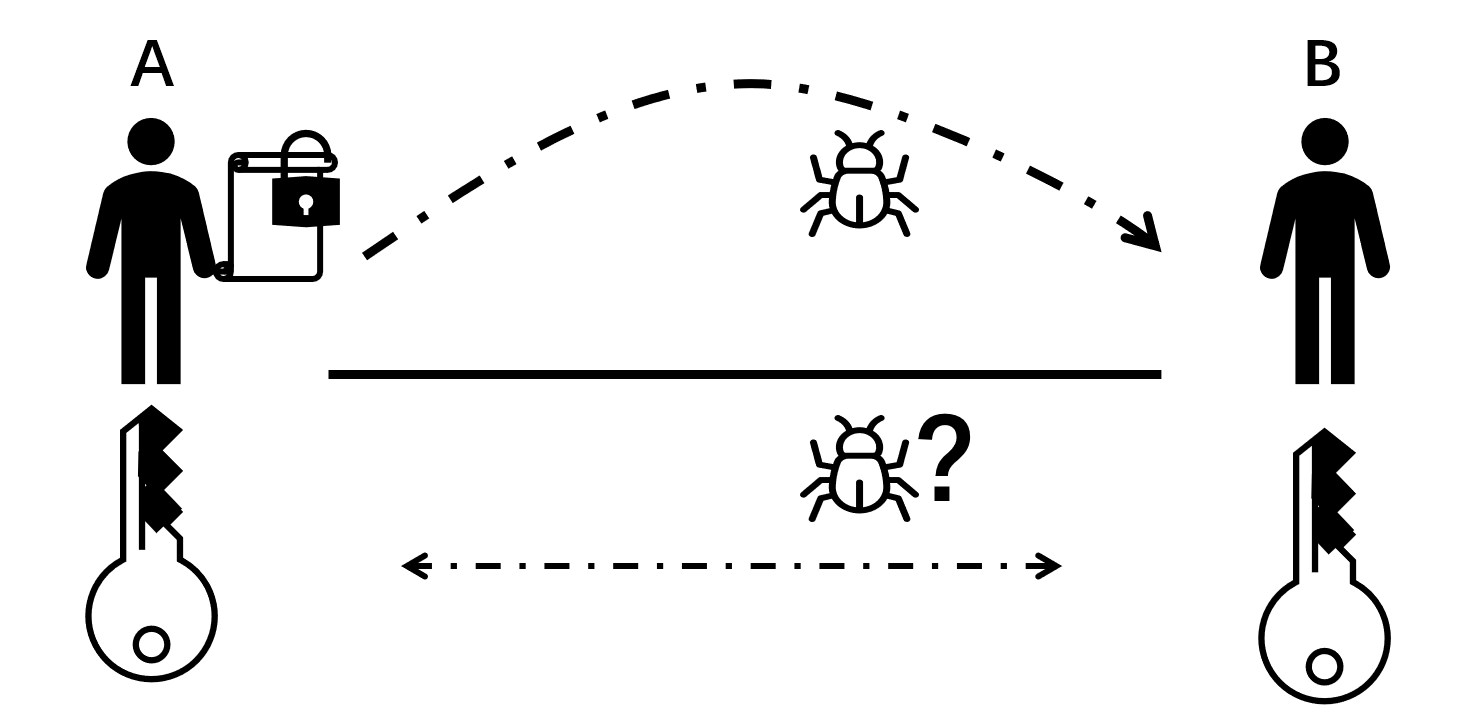
从上文的推导过程得出，如果希望在网络中进行加密通信，就不能单独使用对称加密算法，需要对密钥进行加密或隔离。对于隔离方法，一般就是通过自然人来运输密钥的储存介质。对于加密方法，一般是使用非对称加密算法。由于非对称密码体制的复杂性，一般仅在交换对称密码的密钥时使用非对称加密算法，不直接使用非对称密码体制直接进行加密通信。

非对称加密算法流程为密钥协商，加密，解密。

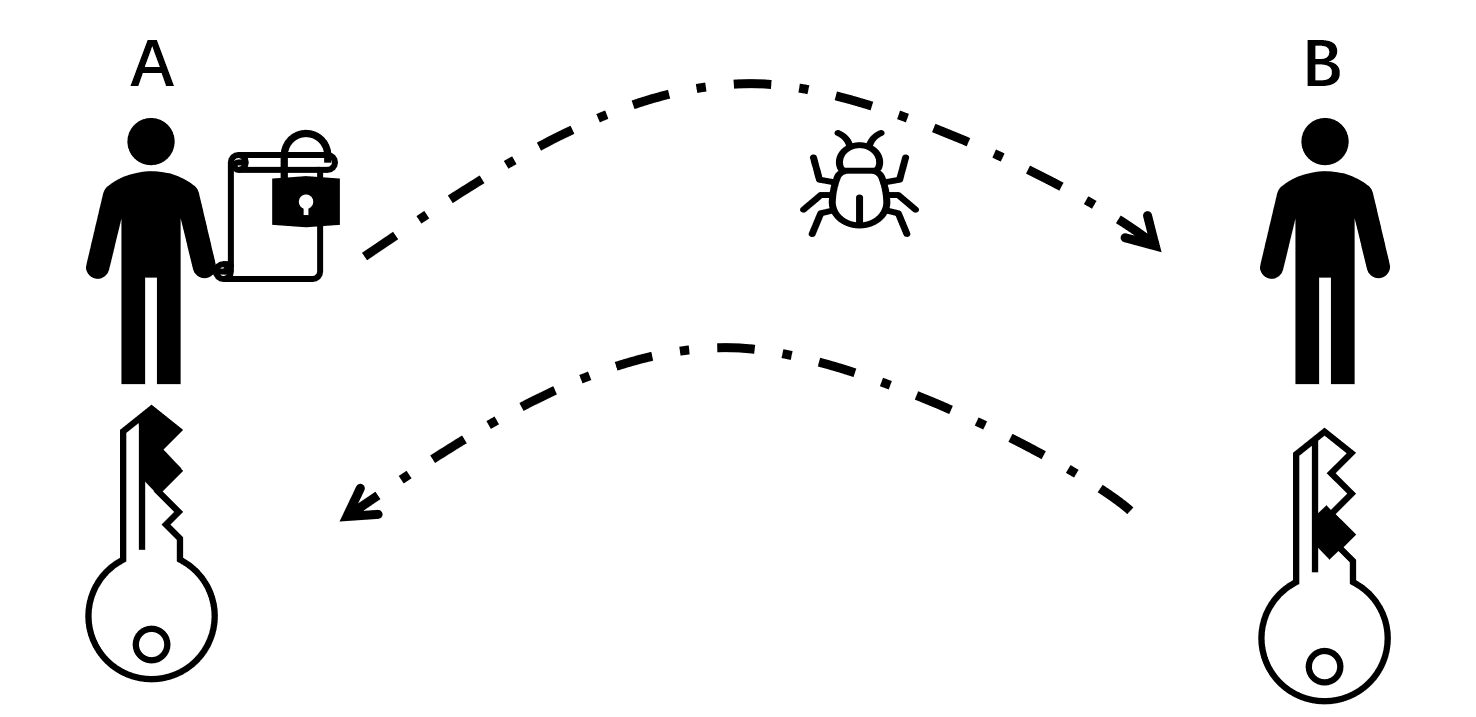
“非对称”，即加密、解密使用的密钥是不同的。假设A希望给B发送信息，密钥协商过后，A拥有的密钥称为公钥，B拥有的密钥称为私钥。公钥用来加密，私钥用来解密。由于只有B拥有私钥，也就只有B能够解密信息，从而保证了通信安全。如果希望双向通信，只需要A、B各自生成一对公私钥，并将公钥发给对方即可。在RSA中，由B生产一对密钥，然后通过网络（无需保密）将公钥发送给A，B自己保留私钥。由于公钥公开了，所以称为公钥。之所以有公钥、私钥之分，主要是RSA算法保留下来的称呼。有些非对称加密算法的两类密钥都可能不公开，但依然称用于加密的密钥为公钥，解密的密钥为私钥。

身份认证引入非对称密码体制

身份认证就是判断一个用户是否为合法用户的过程，最常用的身份认证方式密码认证，即系统通过核对用户输入的用户名和口令与系统中存储的该用户的用户名和口令是否一致，来判断用户身份是否正确。

身份认证的认证方法有三种，基于信息秘密的身份认证，基于信任物体的身份认证，基于生物特征的身份认证。上述三种方法可理解为，你知道什么（独一无二的信息，如密码），你有什么（独一无二的东西，如印章），你身体上有什么（独一无二的部位，如指纹）。对于第三点，认证的是自然人，也就默认：一个自然人对应且仅对应一个（整型）意识。第三种方法不适用于人格分裂的自然人。

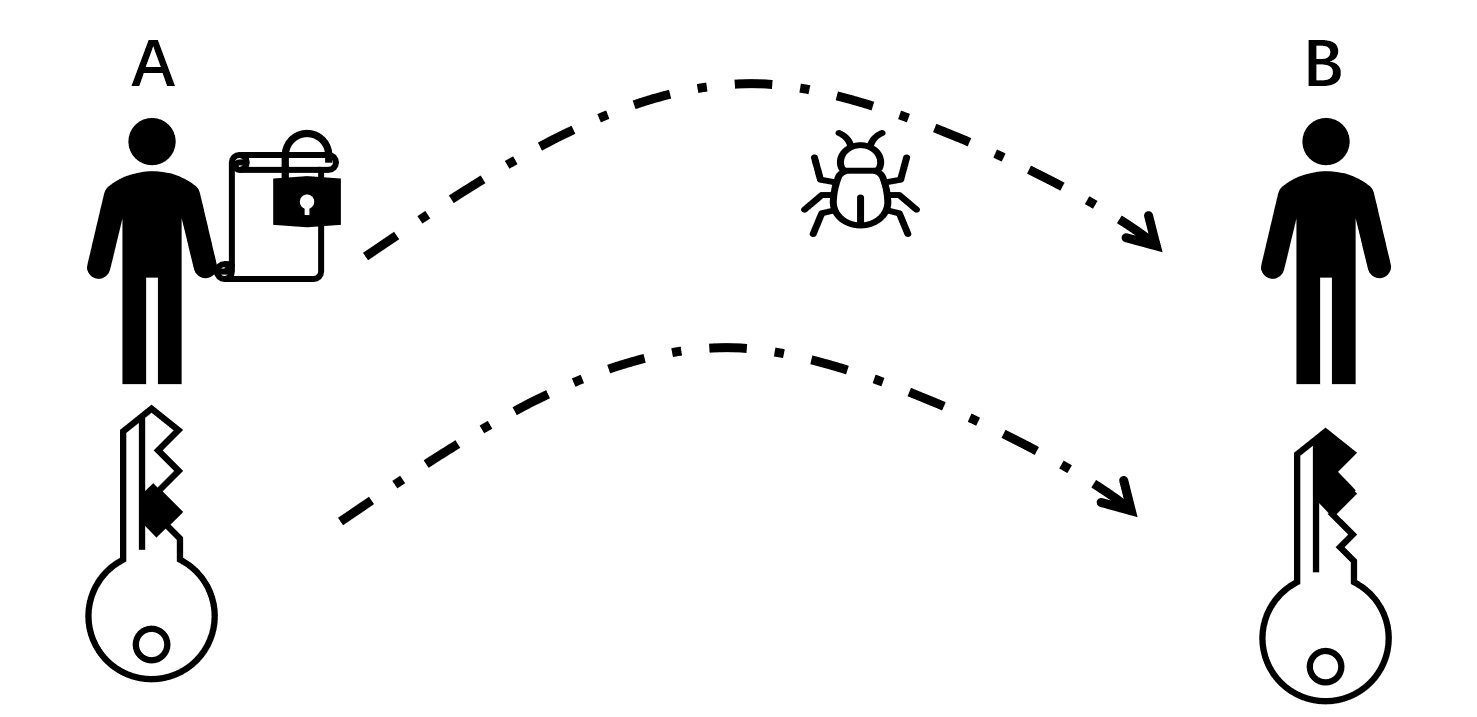
在身份认证中使用的非对称加密是通信中加密方法的逆过程。假设A希望向B证明自己的身份，密钥协商过后，A拥有的密钥称为私钥，B拥有的密钥称为公钥。私钥用来加密，公钥用来解密。认证过程为，A公布原文及密文，B用公钥解密密文，如果解密后的明文与A公布的原文一致，由于只有A拥有密钥，则验证了A的身份。在RSA中，由A生产一对密钥，然后通过网络（无需保密）将公钥发送给B，A自己保留私钥。

信息安全

本段用以阐述保密与信息安全间的关系。

保密的百度百科解释为：一种不让秘密泄露，保守事物的秘密的行为。从信息的角度来看，保护的是01比特的顺序，避免被他人知晓。保密只是信息安全的子集，要做到信息安全需要全方位的保护。

举个保密而不安全的例子。假设蓝绿两军产生冲突，经过一段时间的交火，绿军发现蓝军每次发起攻击前会向战区广播一段“神秘代码”。绿军记录代码，在做好埋伏后也播放了这段“神秘代码”，蓝军手忙脚乱，最后溃败。战后发现，那段“神秘代码”正是蓝军的“发起攻击”命令。蓝军的加密通信确实保护了“发起攻击”四个字本身，却没保护住“发起攻击”的含义。

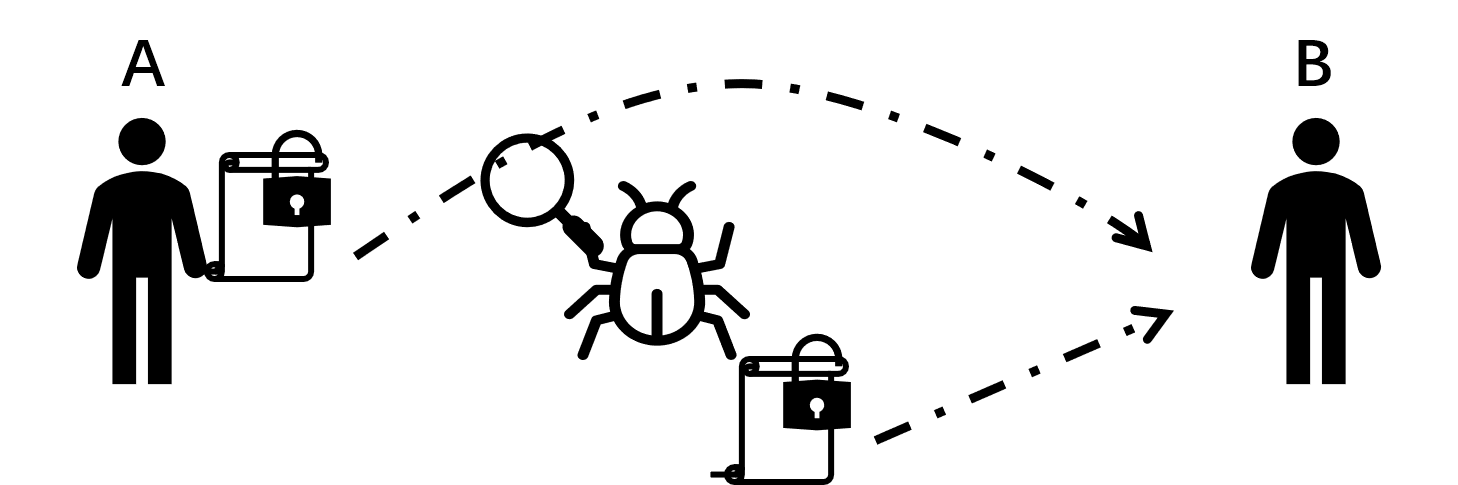
上述攻击方式称为重放攻击，还有伪造、篡改等多种攻击方式，从这个例子可以看出，信息安全远不止加密通信。本文重点讨论加密算法本身，不重点考虑加密外的信息安全。

非对称密码体制

简介中给出了例子，从通俗的角度介绍了非对称密码体制，这里给出实质。设计非对称密码体制，等价于设计或寻找一种陷门单向函数。陷门单向函数要求正向计算简单、反向计算难、已知陷门后反向计算简单。解密密钥就称为陷门。

目前大部分非对称密码算法依赖三种数学难题，大整数质因子分解、离散对数和椭圆曲线。具体内容会在后文详解。

RSA——大整数质因子分解

大整数质因子分解难题

如果 $ n = p * q $，且p与q互质。若只知道n，则很难求出p和q。

欧拉定理

欧拉定理是一个关于同余的性质。如果正整数n和整数a互质，那么就有 $ a^{\phi(n)} \equiv 1(mod \ n) $ ，其中欧拉函数 $ \phi(n) $ 表示小于n且和n互质的正整数个数。如果 $ n = p * q $，且p与q互质，则 $ \phi(n) = (p-1) * (q-1) $ 。

欧拉定理推论

$ a^{\phi(n)} \equiv 1(mod \ n) => $
$ a^{ j * \phi(n) } \equiv 1(mod \ n) => $
$ a^{ j * \phi(n) + 1 } \equiv a(mod \ n) $

规定a小于n。如果a与$ \phi(n) $互质，则上述公式成立。如果a与$ \phi(n) $不互质，则$ a = p $ 或 $ a = q $ ，经过计算，也成立。所以在p与q互质的情况下，a取任意值（规定a小于n）都满足推论公式。

裴蜀（贝祖）定理的重要推论

若e、c互质，则存在d、y两个整数，满足 $ e * d + c * y = 1 => $
$ e * d = 1 - c * y => $
$ (e * d) (mod \ c) = (1 - c * y) (mod \ c) => $
$ (e * d) (mod \ c) = 1 $

RSA算法流程

RSA算法有三个步骤，包括生成密钥、加密和解密。

1.生成密钥

（1） 生成两个不同的大质数p和q。
（2） 计算模数 $ n = p * q $ 和欧拉函数 $ \phi(n) = (p - 1) * (q - 1) $ 。
（3） 计算用于加密的公钥e。满足e小于 $ \phi(n) $ 且互质。
（4） 计算用于解密的私钥d。满足 $ (e * d) (mod \ \phi(n)) = 1 $ 。
（5） 公开e和n，其余保密。

2.加密

规定原文 $ m < n $ （否则需要分组），加密公式如下，c为密文。
$ c = m ^ e (mod \ n) $

3.解密

解密公式如下。
$ m = c ^ d (mod \ n) $

RSA算法说明

1.安全性

RSA算法的安全性基于大整数质因子分解的困难性。从公开的n无法分解出p和q，从而无法计算欧拉公式，也就无法算出私钥。

2.私钥的存在性

生成密钥的第四步，由裴蜀定理可知私钥一定存在。

3.解密的正确性

$ (e * d) (mod \ \phi(n)) = 1 => $
$ e * d = k * \phi(n) + 1 => $

$ m’ = m ^ {e * d} (mod \ n) => $
$ m’ = m ^ {k * \phi(n) + 1} (mod \ n) => $

由欧拉定理推论得知
$ m’ = m $

DH（密钥交换）——离散对数

离散对数难题

给定大质数p和p的一个原根g，则可做下式，其中b和i是整数。已知i，求b不难。已知b，求i很难。
$ b = g^i (mod \ p) $

如果g是p的一个原根，满足下式i取不同值时，计算结果都不同。
$ g^i (mod \ p) \ \ \ (0 \leq i \leq p - 1) $

DH算法流程

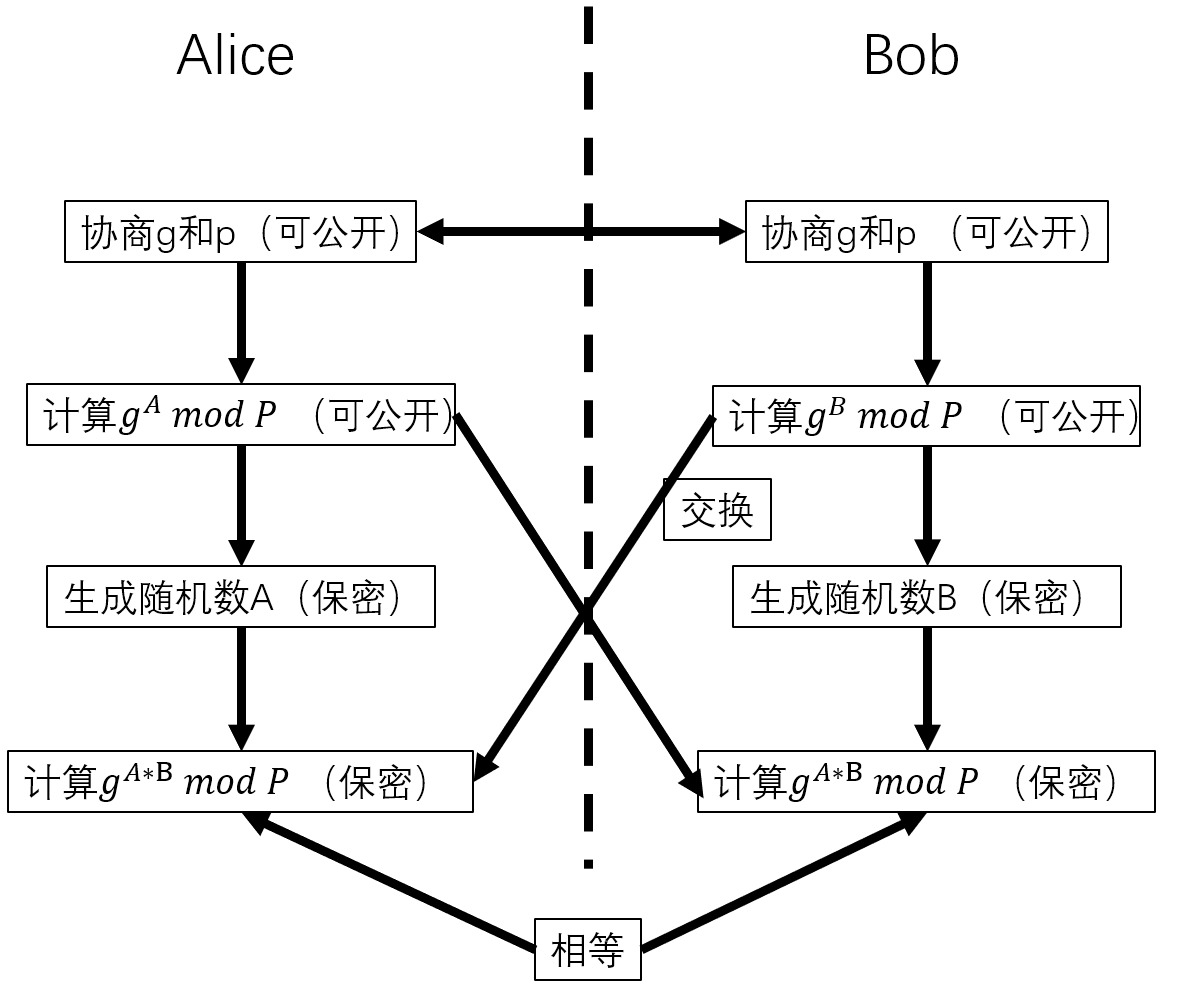
总结

密码永远都不是完全可靠的，所有的加密算法都无法对抗时间。一是所有的密码都是有限的，都可以被暴力破解。二是人类的科技在发展，算力在可预见的未来会一直提升，意味着所有加密算法强度会一直下降。我们要么改变秘密在社会中的地位，要么只能一直研究更好的加密算法。